Els alumnes de primer d’ESO estan estudiant el tema Divisibilitat i els seus professors vam estar buscant propostes interessants per familiaritzar-los una mica més amb els nombres primers i que puguin reconèixer molts d’ells a simple vista. Vam trobar una proposta molt interessant a Illumination, una pàgina nord-americana de recursos per l’ensenyament de les Matemàtiques del National Council of Teachers of Mathematics. Es tractava de fer una espiral començant pel nombre 41, reconèixer que al llarg de la diagonal que va de la part inferior esquerra a la superior dreta anaven apareixent nombres primers i determinar quin és el primer nombre compost que hi apareixia.
Imatge extreta del “brainteaser” esmentat
El problema va sorgir quan el James va trobar aquest vídeo:
I ens vam adonar que amb l’activitat estàvem proposant als alumnes una tasca massa llarga, havien d’escriure els nombres des del 41 al 1681!! Però això tenia una ràpida solució començant l’espiral amb el nombre 11 la tasca que es demana als alumnes és exactament la que preteníem.
De tota manera en la cerca d’aquesta proposta alternativa hem après moltes coses:
- si l’espiral comença amb el nombre x a la diagonal trobarem els nombres n²-n+x quan n=1,2,3,…
- com a màxim després de x talls de l’espiral amb la diagonal trobarem un nombre compost (x²-x+x=x²). Si comencem amb el 41 justament cal 41 talls de l’espiral amb la diagonal per trobar el primer compost i això també passa amb l’11 o el 17 però no passa massa sovint (per exemple, no passa quan el nombre primer no és el primer d’una parella de primers bessons)
A la següent imatge s’ensenyen els elements en que es troben la diagonal i l’espiral quan es varia el nombre primer inicial
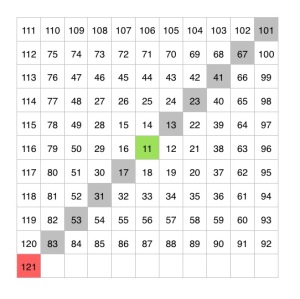
Atenent a que els nombres primers són múltiples de 6 menys 1 o múltiples de 6 més 1, l’espiral serà llarga mentre la serp groga dibuixada a la imatge següent sigui llarga abans d’arribar a un nombre compost:
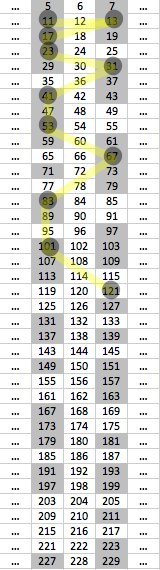Els nombres de la segona columna mai generaran espirals llargues
Departament de Matemàtiques de l'Escola Sadako 